水産資源管理における最適制御理論
[要約]
成長・生残モデルに変分法・最大原理・線型計画法を用いて最適管理方策を検討した。理論的には従来の結果を一般化した解が得られたが、実用的には死亡率を用いた離散型モデルに線形計画法を適用すれば、柔軟に対応することができる。
中央水産研究所・生物生態部・数理生態研究室
[連絡先] 045-788-7638
[推進会議]中央ブロック水産業関係試験研究推進会議
[専門] 資源評価
[対象] 浮魚
[分類] 研究
[背景・ねらい]
水産資源および漁業の特徴は成長過程において連続的に漁獲されることと、自然死亡が大きくてしかもその推定が困難なことである。 人間の管理下におかれ、自然死亡が完全にコントロールでき、また作物の結実後一斉に収穫する農業とは大きく異なる。最近、漁業管理に おいても最適制御理論が導入されいろいろ検討されているが、水産生物の成長と最適制御手法である変分法・最大原理・線型計画法を適用 し、その実用性や従来の手法との整合性を検討した。
[成果の内容・特徴]
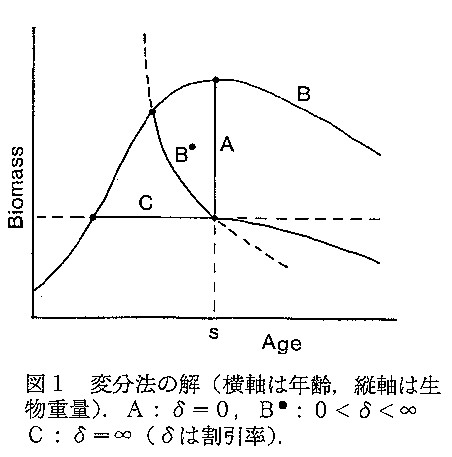
- 変分法では制御変数に何の制限もつけない。したがって漁獲係数Fを制御変数として成長・生残モデルに適用すると、生物重量が最大 になる時点において、瞬間的にすべてを漁獲する「インパルス制御」が最適となる。これは養殖業において実行されている。経済効果とし て割引率と費用関数を導入すると、結果は数学的には異なってくるが、実用的にはインパルス制御と大差ない。 (図1)
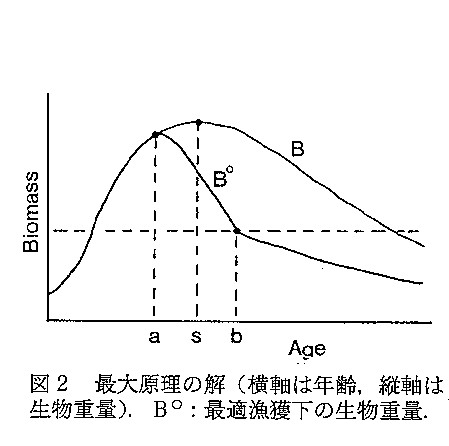
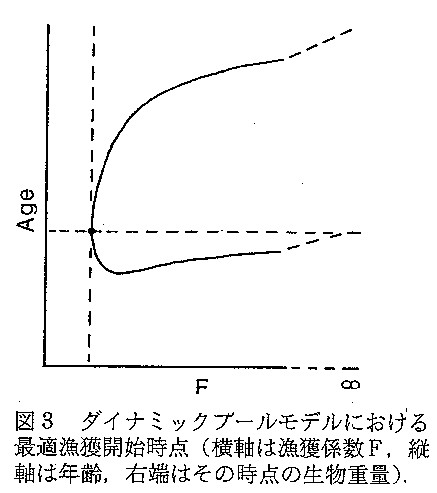
- 通常の漁業ににおいては漁獲係数Fに上限が存在する。そのような制限下では変分法は適用できないため、最大原理を適用する。こ れによりある一定期間ではFを最大に、それ以外ではF=0という最適制御が得られる(図2)。これは 従来のダイナミックプールモデルの結果の一般化となっており、最適制御化では「その時点の生物重量とその後漁獲重量が等しくなる時点 」が最適漁獲開始時点となる(図3)。
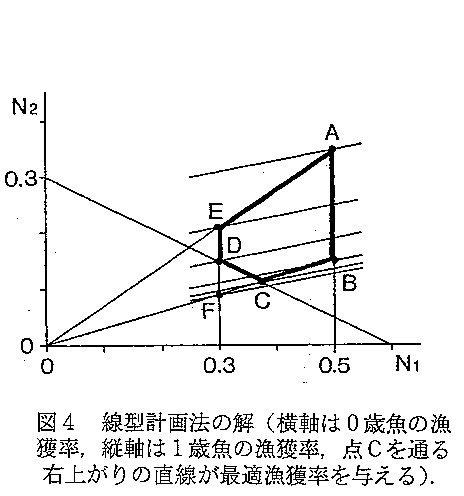
- 総産卵量を一定値以上確保するという条件を加えたような場合、最大原理では数値計算が必要となる。しかし漁獲係数Fのかわりに漁 獲率Eを用いる離散型モデルでは、このような場合はすべて線型計画法で解くことができる(図4)。自 然死亡は推定困難なため一定値を仮定することが多いので、実用的には離散モデルで十分である。
[成果の活用面・留意点]
- 最大の問題は自然死亡が推定困難な場合が多いことで、そのような場合には実際の漁獲を通じて資源状態を推定するフィードバック 的な管理が必要である。また再生産についても確保すべき総産卵量を確定できない場合が多いため、むしろ総漁獲量一定という条件下にお いて、総産卵量を最大にする漁獲方策を検討する方が現実的だろう。線型計画法ではそのような場合にも柔軟に対応可能である。
[具体的データ]
[その他]
研究課題名:資源・漁業の管理技術の確立
漁業管理技術の資源学的基盤の確立
動的計画法による変動する資源の最適管理方策予算区分 :経常研究期間 :平成7~9年度研究担当者:須田真木,赤嶺達郎,岸田 達発表論文等:赤嶺達郎(1996)離散型漁獲方程式と線型計画法.水産海洋研究、60(3),252-258 赤嶺達郎(1997)成長・生残モデルにおける最適制御理論.中央水研報告,10,135-167


